En abril de 1982, el profesor Dan Shechtman, del Technion–Israel Institute of Technology, hizo el descubrimiento que más tarde le valdría el Premio Nobel de Química de 2011: el cristal cuasiperiódico. Según las mediciones de difracción realizadas con un microscopio electrónico, el nuevo material parecía “desorganizado” a escalas más pequeñas, pero con un orden y una simetría distintos a escala mayor.

Esta forma de materia se consideraba imposible, y se tardó muchos años en convencer a la comunidad científica de la validez del descubrimiento. Los primeros físicos que explicaron teóricamente este descubrimiento fueron el profesor Dov Levine, entonces estudiante de doctorado en la University of Pennsylvania y ahora miembro del cuerpo docente del departamento de Física del Technion, y su asesor, el profesor Paul Steinhardt.

La idea clave que permitió su explicación fue que los cuasicristales eran, de hecho, periódicos, pero en una dimensión superior a aquella en la que existen físicamente. Utilizando esta comprensión, los físicos pudieron describir y predecir las propiedades mecánicas y termodinámicas de los cuasicristales.

El Teseracto

Cubo tetradimensional (llamado tesseracto) sobre una superficie dorada con simetría quíntuple. El patrón plasmónico bidimensional cuasicristalino puede reconocerse bajo el teseracto. La imagen representa la proyección de un cubo regular tetradimensional sobre un plano bidimensional cuasicristalino. Crédito de imagen: Florian Sterl, Sterltech Optics

El concepto de dimensión espacial superior amplía nuestro espacio tridimensional familiar (largo, ancho y alto) al introducir direcciones adicionales que son perpendiculares a las tres. Esto es difícil de visualizar, ya que solo podemos percibir el mundo que nos rodea como un espacio tridimensional, y aún más difícil de medir. Un ejemplo de objeto tetradimensional es el teseracto, también conocido como hipercubo.

Al igual que un cubo consta de seis caras cuadradas, un teseracto consta de ocho celdas cúbicas. Aunque no podemos visualizar completamente un teseracto, podemos representarlo a través de sus proyecciones, de forma muy similar a como se ve la sombra de un cubo tridimensional en una hoja de papel bidimensional.

En un nuevo estudio publicado en Science, investigadores del Technion, junto con la University of Stuttgart y la University of Duisburg-Essen en Alemania, arrojan nueva luz sobre este fenómeno. El grupo de investigación demostró que los cristales de dimensiones superiores no solo dictan las propiedades mecánicas de los cristales cuasiperiódicos, sino que también determinan sus propiedades topológicas.

La topología es una rama de las matemáticas que investiga las propiedades geométricas que permanecen inalteradas bajo deformaciones continuas. La topología de espacios de dimensiones superiores se centra en las propiedades de los objetos en más de tres dimensiones y puede ayudar a los investigadores, por ejemplo, a estudiar la estructura del universo y a desarrollar algoritmos de computación cuántica.

Cristal de cuarta dimensión

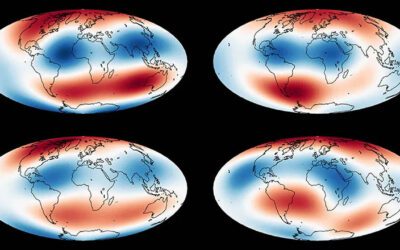
Los investigadores examinaron patrones de interferencia cuasiperiódicos de ondas electromagnéticas superficiales y descubrieron, para su sorpresa, que aunque los patrones parecían diferentes, sus propiedades topológicas en dos dimensiones no podían utilizarse para diferenciarlos. Descubrieron que la única forma de distinguir entre los patrones era haciendo referencia a un cristal “original” de mayor dimensión.

Proyección de un cristal regular tetradimensional sobre un plano bidimensional. Surge una simetría cuasi-cristalina quíntuple. Crédito de imagen: Florian Sterl, Sterltech Optics

Este descubrimiento concuerda con la explicación dada por Levine y Steinhardt, que se basaba en un descubrimiento anterior del matemático británico Sir Roger Penrose (Premio Nobel de Física 2020) y transmitido posteriormente por Nicolaas de Bruijn.

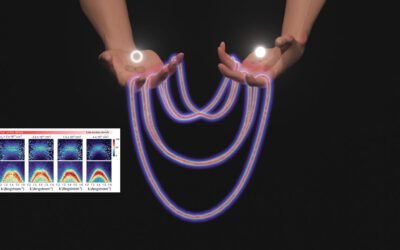
Los investigadores también descubrieron otro fenómeno intrigante: dos patrones topológicos diferentes de ondas superficiales parecían idénticos cuando se medían después de un intervalo de tiempo específico. Este intervalo era extremadamente corto, medido en attosegundos, una milmillonésima de una milmillonésima de segundo. La teoría original de Levine y Steinhardt explica de nuevo este fenómeno como una “competición” entre las propiedades topológicas y termodinámicas (energéticas) de los cristales.

Los hallazgos se lograron utilizando dos métodos: microscopía óptica de barrido de campo cercano realizada en el laboratorio del profesor Guy Bartal por el Dr. Kobi Cohen y microscopía electrónica de fotoemisión de dos fotones, medida en colaboración entre la Universidad de Stuttgart y la Universidad de Duisburg-Essen en Alemania. Los descubrimientos reportados en el manuscrito allanan el camino para nuevos métodos para medir las propiedades termodinámicas de los cristales cuasiperiódicos.

En un futuro próximo, los investigadores planean ampliar sus hallazgos a otros sistemas físicos y examinar más profundamente la interacción entre las propiedades termodinámicas y topológicas. Potencialmente, las propiedades topológicas únicas de las cuasicristales, de dimensiones superiores, podrían utilizarse en el futuro para representar, codificar y transferir información.

Los hallazgos de la investigación titulada “Four-dimensional conserved topological charge vectors in plasmonic quasicrystals” han sido publicados en la revista Science.

Resumen:

La simetría y la topología de los sistemas físicos están estrechamente relacionadas con las simetrías que rigen las propiedades topológicas. Los cuasicristales son sistemas ordenados, pero no tienen simetrías de traslación ni de rotación. El trabajo teórico ha demostrado que los cuasicristales pueden entenderse como la proyección de un cristal de mayor dimensión en un espacio de menor dimensión. Al entrar en el espacio tetradimensional y proyectarlo hacia abajo en dos dimensiones, la compleja dinámica de las ondas de luz en el cuasicristal plasmónico exhibió movimientos de vectores de carga topológica tetradimensionales y leyes de conservación de carga topológica asociadas. Este enfoque permite el estudio de sistemas topológicos en dimensiones superiores.

[FT: uni-stuttgart.de]

¿Te gustó este contenido? Te invito a compartirlo con tus amigos. Síguenos en nuestra Página de Facebook, para recibir a diario nuestras noticias. También puedes unirte a nuestro Grupo Oficial y a nuestra comunidad en Telegram. Y si crees que hacemos un buen trabajo, considera apoyarnos.